Riken 実用理科技能検定
理検|理科検定

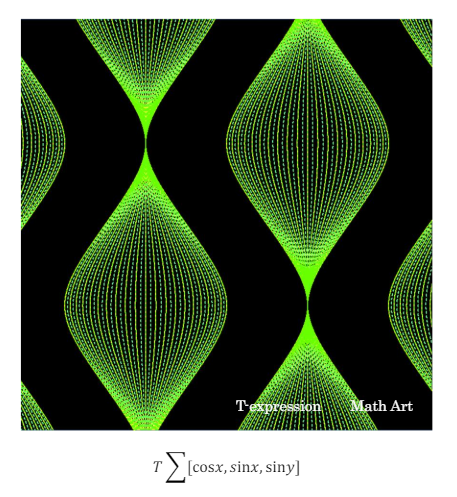
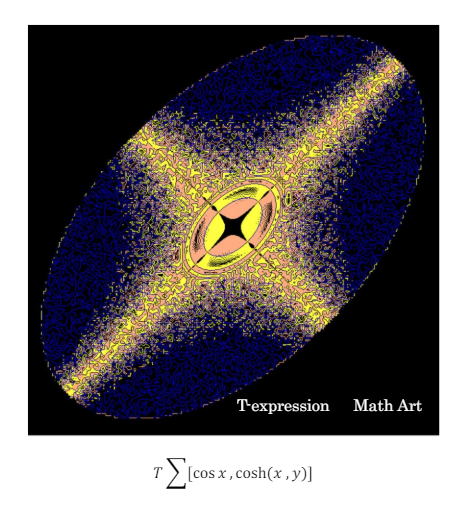
T-expression
Graphic Design
Math Art

\[T\sum [\sin(x^2+y^2)=t]\]Trigonometric function “ sine or cosine ” expresses periodicity. Quadratic expression "\(\left(x^2+y^2\right)\)" shows circular shape.
Expression factor "\(t\)" associates these characteristics.
T-expression , Math Art skill is investigated by TAKADA Tashiyoshi in 2000.

In this case, it is different to see through a microscope. The expression is clear whole around. Moreover all patterns are different each other. And the interference stripes emit a characteristic beauty. \[T\sum[\sin \left(x^2-y \right)\cos \left(x-y^2 \right)=t]\]

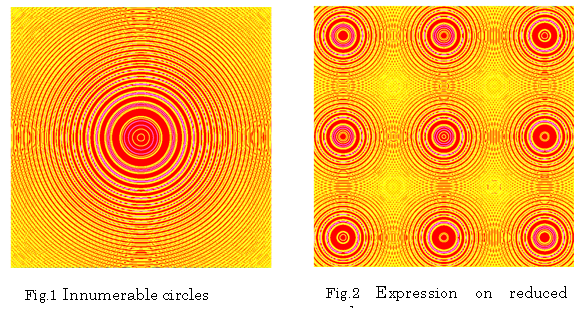
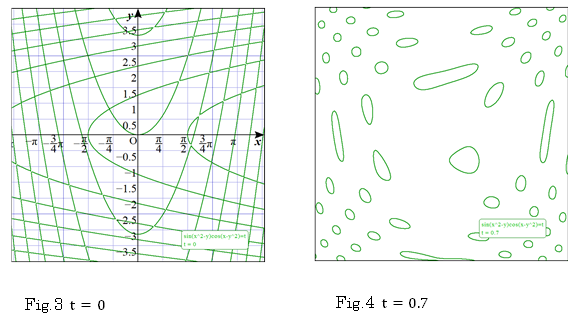
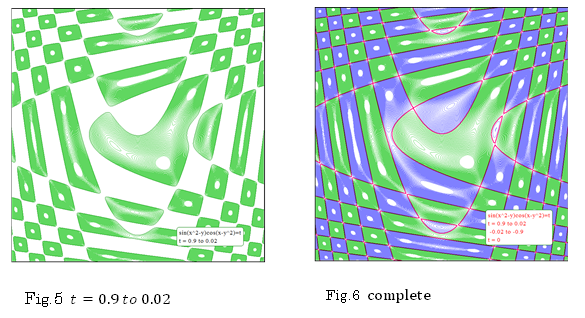
Fig.6 T-expression is designed; \(t=0\) red \(t=0.9\) to \(0.02\) green
\(t=-0.9\) to \(-0.02\) blue Periodic feature is represented with sine, cosine function and two parabolic features cross at right angles. If you reduce the expression Fig.6, you may find another world.
" \(x\sin t + y\cos t\) " called rotation structure makes rotate a shape with a center of the origin either clockwise or counterclockwise.
Fig.9 \(x\sin t + y\cos t =x^2+y^2\) ;90 circles make yellow round cookie.
Fig.10 \(x\sin t + y\cos t = x^2+y^2-3\) ;90 circles make magenta doughnut.

T-expression

• T-expression